Pythagoras Theorem Proof

Pythagoras Theorem Statement

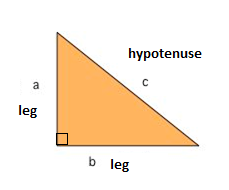
Pythagoras theorem states that “In a right-angled triangle,  the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangles have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°. The sides of a right triangle (say x, y and z) which has positive integer values, when squared are put into an equation, also called a Pythagorean triple.

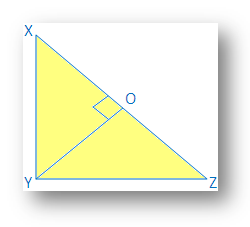
Proof: First, we have to drop a perpendicular BD onto the side AC

We know, △ADB ~ △ABC

Therefore, ADAB=ABAC (Condition for similarity)

Or, AB2 = AD × AC ……………………………..……..(1)

Also, △BDC ~△ABC

Therefore, CDBC=BCAC (Condition for similarity)

Or, BC2= CD × AC ……………………………………..(2)

Adding the equations (1) and (2) we get,

AB2 + BC2 = AD × AC + CD × AC

AB2 + BC2 = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC2 = AB2 + BC2

Hence, the Pythagorean thoerem is proved.

Note: Pythagorean theorem is only applicable to Right-Angled triangle.