Triangles, Exterior Angle Theorem

Exterior Angle Theorem

The exterior angle theorem states that if a triangle’s side gets an extension, then the resultant exterior angle would be equal to the total of the two opposite interior angles of the triangle.

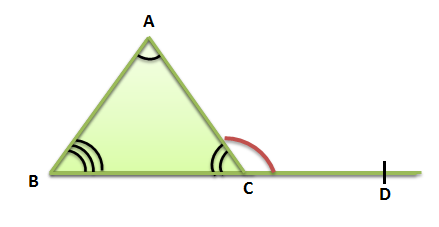
Fig. 2 Exterior Angle Theorem

According to the Exterior Angle Theorem the sum of measures of ∠ABC and ∠CAB would be equal to the exterior angle ∠ACD . General proof of this theorem is explained below:

Proof:

Consider a ∆ABC as shown in fig. 2, such that side BC of ∆ABC is extended. A line, parallel to the side AB is drawn as shown in the figure.

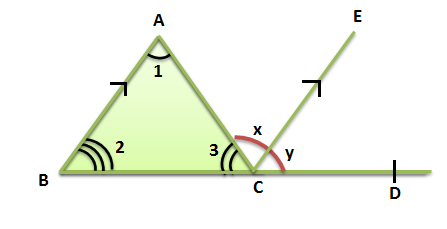
Fig. 3 Exterior Angle Theorem

S. No	Statement	Reason
1.	∠CAB = ∠ACE ⇒∠1=∠x	Pair of alternate angles((BA¯¯¯¯¯¯¯¯) ||(CE¯¯¯¯¯¯¯¯) and (AC¯¯¯¯¯¯¯¯) is the transversal)
2.	∠ABC = ∠ECD ⇒∠2 = ∠y	Corresponding angles ((BA¯¯¯¯¯¯¯¯) ||(CE¯¯¯¯¯¯¯¯) and (BD¯¯¯¯¯¯¯¯)) is the transversal)
3.	⇒∠1+∠2 = ∠x+∠y	From statements 1 and 2
4.	∠x+∠y = ∠ACD	From fig. 3
5.	∠1+∠2 = ∠ACD	From statements 3 and 4

Thus, from above statements it can be seen that exterior ∠ACD of ∆ABC is equal to the sum of two opposite interior angles i.e. ∠CAB and ∠ABC of the ∆ABC.